- 相关推荐
穿越到拿破仑部下当参谋
穿越到拿破仑部下当参谋东台市实验中学教育集团 八年级(14)班 朱灵铃
同学们知道,拿破仑是一位伟大的军事家,他英勇善战,是世界军事史上的奇人,同时他还具有卓越的数学才能。在学习“全等三角形”时,崔老师给我们讲了拿破仑的一个故事,大意是:1805年,拿破仑指挥的法国军队与德俄联军在莱茵河畔激战, 德俄联军在莱茵河北岸A处(如图1), 而法国军队在河的南岸,中间隔着一条很宽的莱茵河,法国军队要想使炮弹准确地落在对方的阵地上,就必须知道河有多宽。聪明的拿破仑站在南岸的点O处反复观望,发现河水与北岸的边线在视线里恰好擦着他的帽舌边沿,于是眉头一皱,计上心来。他牢记住眼睛到对岸水边的“距离感觉”,立即转身,再次寻找那个“距离感觉”和视觉里恰好擦着他的帽舌边沿的那一点,然后立即叫人把这个地方到莱茵河南岸水边的距离丈量一下。他知道,量出的距离一定等于河的宽度,于是他下令根据这个长度对德俄联军发起炮击,果然命中了目标。崔老师告诉同学们,拿破仑的做法并不神秘,他是利用三角形全等的知识解决的,由拿破仑的做法知,∠APO=∠BPO,PO=PO,∠AOP=∠BOP=90°,这样根据“ASA”就能得到△APO≌△BPO,从而BO=AO。最后崔老师还以玩笑的口气说,拿破仑作为法军的最高指挥官,这类事应该由他手上的参谋来做,假如时光倒流,让你穿越到拿破仑手上当参谋,你能不能帮他解决这一类问题呢?
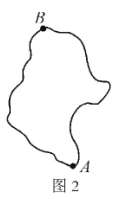
法军的新问题:如图2,A、B两点位于法军某训练基地的两端,法军想用绳子测量A、B间距离,但是A、B两点之间不可直接到达。你能帮法军设计测量方案吗?如不能,说明困难在哪里;如果能,写出方案,并说明其中的道理。
朱参谋的分析:此题的测量方法很多,我们可以用我们刚刚学会的全等三角形的知识来解决,构造出全等三角形,把AB“搬”出来测量,短绳子多量几次也就可以了。
测量方案1:
(1)先在地面上另找一个可以直接到达A点和B点的点C;
(2)连接AC并延长到点D,使CD=CA;
(3)连接BC并延长到点E,使CE=CB;
(4)连接DE,并测出它的长度。
如图3,DE的长度就是A、B间距离。
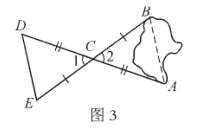
【理由】在△ABC和△DEC中,CB=CE,∠2=∠1,CA=CD,∴△ABC≌△DEC(SAS)。∴ AB=DE.
测量方案2:
(1)在AB的垂线AF上取两点C、D,使CD=AC;
(2)过点D作AF的垂线DG,并在DG上取一点E,使点B、C、E在同一条直线上;
(3)这时测得DE的长,就是A、B间的距离。
如图4,DE的长度就是A、B间距离。
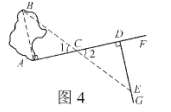
【理由】连接B、C、E,∵点B、C、E在同一条直线上,∴ ∠1=∠2,∵AB⊥AF,DG⊥AF,∴∠BAC=90°=∠GDC.
在△ABC和△DEC中,∠BAC=∠EDC,CA=CD,∠1=∠2,∴△ABC≌△DEC(ASA)。∴ AB=DE.
崔老师的点评:运用“全等”测量距离的问题,应根据实际问题情境,以全等三角形的知识为载体,建立数学模型,再运用数学模型求解。生活中的实际问题的解决办法往往不止一种,具体选用方法时,应考虑具体情况。另外在实际测量时,最好是重复2~3次后求平均数,以避免较大的误差。本题来源于课本,来源于生活,可以激发学生“学有用的数学”,更能激发学生的学习热情和创新热情以及求知欲望,让学生在创造中养成应用数学的意识。
【穿越到拿破仑部下当参谋】相关文章:
拿破仑的语录12-14
拿破仑的名言08-23
拿破仑名言08-23
拿破仑经典的语录11-12
参谋长述职报告01-09
我穿越到了作文05-15
穿越到3011年作文08-24
拿破仑经典语录08-24
我穿越到了秦朝作文07-19
参谋长述职报告5篇02-23